동적 계획법 정의
동적계획법(Dynamic Programming) 개념
동적계획법이란, 큰 문제에 대한 해답을 얻기 위해 해당 문제를 크기가 더 작은 문제들로 쪼개어, 작은 문제들을 먼저 해결한 뒤 그 결과들을 이용해서 원래의 큰 문제를 해결하는 기법을 의미한다.
정리하면, Dynamic Programming에서의 핵심은 문제를 잘개 쪼개 조그마한 단위에서의 해결 방법을 구해(점화식) 그것이 최종적인 솔루션과 같은 형태로 구성될 수 있도록 설계하는 것이다.
동적계획법 문제풀이의 예시 - 점화식
동적계획법은 점화식만 구하면 된다. 아주 간단한 피보나치 수열의 경우로 예를 들어보자.
n-1번째 수와 n-2번째 수의 합이 n번째 수가 되므로, 재귀를 이용하거나 배열에 저장하는 형태로(즉 초기에 답을 구해놓은 것을 활용하는 형태로) 최종적인 답을 얻을 수 있다.
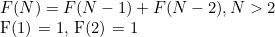
피보나치 수열의 점화식과 초기조건.
어떤 형태로든 점화식으로 문제를 풀어낼 수만 있다면, 해당 점화식을 코드로 구현하기만 하면 된다.
(모든 문제가 점화식으로 구현되지는 않지만 점화식이 떠오른다면 어렵지 않게 된다.)
참고로 피보나치 수는 Memoization의 방식, Tabulation 방식으로 해결할 수 있다.
Memoization은 해당 i번째 피보나치 수를 구했는지를 확인해서 반환하며 재귀적으로 해결하는 탑다운 방식이고, Tabulation은 for문으로 반복적으로 앞에서부터 배열을 채워나가는 바텀 업 방식이다.
동적계획법 문제 접근 시 유의사항
- DP 문제는 대부분 1차원, 2차원 dp배열을 생성하고 점화식에 맞게 그 배열을 채워나가는 형태로 문제를 해결한다.
- 또한 점화식은 대부분 max, min을 통한 dp배열 값 +- input 값의 비교연산으로 세울 수 있다.
- max, min 연산의 원활한 비교를 위해 dp배열의 초기 값은 INT_MIN, INT_MAX(#include <climits> 필요)으로 설정해두는 것이 좋다(값이 너무 큰 것이 싫다면 나오지 않을 것 같은 값 중에서 가장 크거나 작은 수(ex. 9999, -1)로 보기 편하게 설정해두자)
- (어려움) dp배열을 채워넣는 점화식 설계 시 비교해야 할 조건들이 무엇인지를 항상 유의해야한다.
1. 비교해야할 정보가 1개면 dp배열은 1차원 배열로 설계할 수 있다(ex. 백준 11057 오르막 수, 2294 동전 2 등)
2. 비교해야할 정보가 2개면 dp배열은 2차원 배열로 설계해야 한다(ex. 백준 9465 스티커, 1149 RGB거리 등)
DP는 문제를 잘게 쪼개서 해결하는 것이다. 따라서 dp배열은 문제의 일부분에 대한 답들을 항상 가지고 있어야 한다.
이게 무슨 말이냐면, dp배열의 i, j 의 값은 dp배열의 i-1과 j-1 의 정보를 가지고 채워넣을 수 있어야 한다는 말이다(+여기에 max, min, input 값 연산이 추가되는 것)
따라서 원하는 최소, 최대의 값을 얻기 위해 비교해야할 정보가 무엇인지를 빠르게 확인하는 연습을 해야 한다. - dp배열 설계 시, 무조건 마지막 i, j 의 값이 최대 혹은 최소의 값을 가지지 않아도 된다. 마지막 i 행에서의 값들을 정렬해서 최대 혹은 최소를 출력하면 된다.
dp배열은 문제를 쪼개서도 해결할 수 있도록 도와주는 수단일 뿐이지, 그 자체가 정답이 될 필요는 없다. - 다이나믹프로그래밍 문제가 어렵게 출제된다면, dp배열의 점화식 i, j 의 조건이 까다롭게 출제될 것이다(ex. 백준 9456 스티커)
문제 유형 정리
아래 문제 유형들은 www.codetree.ai/ 와 https://www.youtube.com/channel/UChMuqvL1w8wgeacH_r0QLsg 에서 참고하였습니다. 문제가 될 경우 삭제하겠습니다.
격자 안에서 한 칸씩 전진하는 DP
진행하다 끊기고 또 진행하다 끊기는 DP
조건에 맞게 선택적으로 전진하는 DP
--- 얘네는 정리 필요
아이템을 적절히 고르는 문제 - 동전 거슬러주는 문제. 최대 동전의 수 구하기 OR 최소 동전의 수 구하기
최대 동전의 개수를 구하기: 원하는 M이란 값을 만들기 위해서, 현재까지 동전의 개수만 신경쓴다. 지금까지 사용한 동전의 개수가 많을 수록 좋은 것. max라고 들어갈 것이므로, 0과 같은 minimum 값을 넣으면 된다.
문제
- N개의 동전을 가지고 금액 M을 만들기 위해 필요한 최소/최대 동전의 수 구하기. 같은 동전을 여러 번 사용할 수 있음.
ex. N = 4, M = 12, coin = {1, 3, 5, 6}
비교해야할 대상
- 내가 지금 얼마의 금액을 만들었는가?
- 몇 개의 동전을 사용하고 있는가?
→ 1차원 배열의 j index: 만든 금액, dp[j] = 사용한 동전의 최소 개수
초기화:
- 최소 동전의 개수일 때: 주어진 coin[i] 값에 해당하는 dp의 j index에 1을 표기. 나머지 항에는 INT_MAX.
해당 값에 + 연산을 수행하지 않을 것이므로, overflow 발생하지 않는다.
점화식:
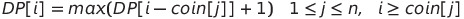
아마 최대 동전의 개수를 구하는 문제는 없을 것 같다..
연속적이지만 직전 상황에 영향을 받는 DP - 백준 9465 스티커, 1309 동물원
연속적으로 고를 수 없는 상황에서 최대의 결과를 낼 수있도록 설계해야하는 문제이다.
문제
- N개의 옷을 M일 동안 적절히 입어 만족도가 최대가 되도록하려고 한다. 각 옷은 입을 수 있는 기간이 정해져 있다. 같은 옷을 여러 번 입어도 된다. 만족도는 각 인접한 날에 입은 옷의 v 값 차이이다.
문제 링크: https://www.youtube.com/watch?v=n3ZmcyGqCeo
비교해야 할 대상
- 현재 날짜가 언제인지?
- 현재 입고 있는 옷이 무엇인지?
→ 2차원 DP 문제가 된다.
DP[i][j] 가 의미하는 값: i 날짜에 j 번째 옷을 입고있을 때 가지는 최대의 만족도.
초기화
- max 값을 가지려고 하는 것이므로, -1 또는 INT_MIN 값으로 초기화.
- 옷을 입을 수 있는 기간이 정해져있고, '만족도'는 이전 옷과의 v값 차이이므로, DP[1][j] 에서 j 번째 옷을 i=1일 때 입을 수 있는 j에 대해서만 0으로 초기화.
점화식
- 범위 내에 있는 모든 j에 대해 max값을 찾아야 하므로, for loop를 동작시킨다.
- DP[i][j]의 값을, i번째 날에 j번째 옷을 입을 때의 최대 만족도로 정의하기로 하였음을 기억하자.
i-1번째 날에 입은 k번째 옷에 대한 value와의 차이의 최대를 구해야 한다.


원하는 State를 정의하여 한 칸씩 나아가는 DP - ex. 둘 중 하나 잘 고르기 어렵다!
고려해야하는 상태가 2가지임에 주의해야 한다. 동전 최대 개수를 구하는 것에서 고려해야 했던 것은 '지금까지 선택한 동전의 합'이 같다면, 동전의 개수가 더 많은(max) 것을 dp에다가 쓰면 됬었다. 즉, 비교해야할 것이 1가지 였다.
그러나 여기에서는 비교해야하는 상태가 2가지이다. 언제의 최대를 구하냐면,
지금까지 고려한 숫자의 위치가 같은가?
지금까지 선택한 숫자의 개수가 같은가? 그렇다면 지금까지의 홀+ 짝- 연산의 결과의 최대를 DP에 쓴다.
따라서 이중 배열의 DP가 된다!
같은 개수의 숫자를 고른 상태에서 비교해야 하므로, j-1로부터 값을 가져온다...
(현재의 수를 더하고 빼는 것으로 max를 구하는 approach는 본인이 한 것과 유사하나, 본인의 접근은 idx를 기억하지 못한다는 것에서 문제가 있었다)
문제풀이는... 격자안에서 한 칸씩 전진하는 DP 와 같은 것 같다.
문제 1
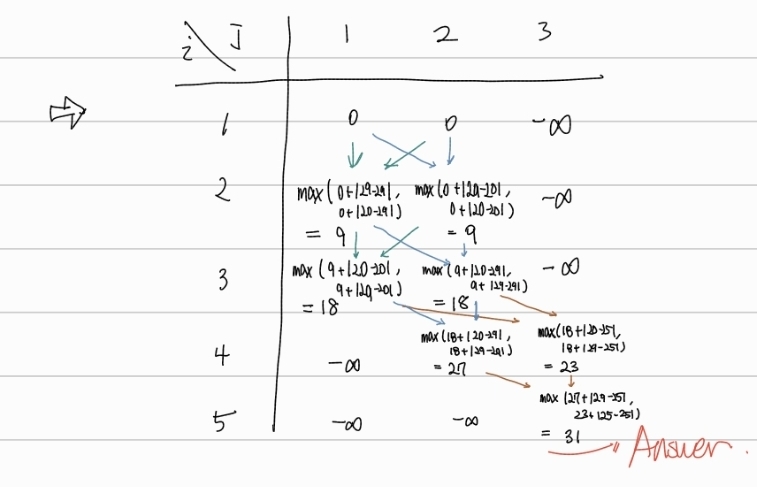
- 2*N 개의 숫자 중 N개를 적절히 골라, 홀수 번째 수는 더하고, 짝수 번째 수는 빼서 총 합이 최대가 되도록 하기
ex. N = 5, input = {2, 3, 4, 3, 5, 9, 1, 10, 9, 6}.
{4, 3, 9, 1, 10} 순으로 선택하면 19로 최댓값이다.
문제 링크: https://www.youtube.com/watch?v=QmkpjkyqTXU&t=410s
비교해야할 대상
- 내가 지금까지 몇 개의 숫자를 뽑으려고 하는지, i index→ 나중에 N번째 i에서의 최댓값을 리턴하기 위함.
- 현재 고려하고 있는 숫자가 몇 번째 수인지, j index
(밑의 해설 이미지에서는 몇 개를 뽑으려고 하는지가 j index로 설정되어 있음)
문제가 잘게 쪼개지는지를 확인해야한다. j번째의 수를 고려한다 == 주어지는 숫자의 개수가 증가해도 bottom-up approach 가 된다.
★ 중요 ★ 무엇을 비교해야하는가를 생각할 것. 주어진 문제가 1차원 배열이라 DP를 2차원으로 만들어야하는지 알기 어렵다. DP 배열의 i, j 는 비교할 사항들을 의미한다. 대개 2가지 조건을 기준으로 답을 구할 수 있다(2차원 DP 배열)
초기값
- 최댓값을 구하는 문제이므로 INT_MIN으로 초기화. 나중에 INT_MIN + alpha 연산을 하므로 overflow X
이전인덱스에서의 값을 더해오는 것이므로, j 번째 수를 고려하는 중에 i개를 뽑는 경우에 대해, i j 인 값은 모두 0으로 초기화.
풀이 및 점화식: 아래 이미지들을 참고
- i 는 input으로부터 i 개의 숫자를 뽑아 연산에 포함시키는 index이므로, 홀수인지 짝수인지의 구분은 i%2 == 0 ? false:true 로 계산한다.

초기 접근)

맞는 접근) 내가 고려하는 숫자의 개수(i)를 알아야하고, 그중에서도 연산하고자 하는 수(j)를 카운트해야한다.

j가 연산에 직접적으로 관여하는 인덱스이다. 따라서 j가 홀수이면 dp에서 덧셈을 하고, j가 짝수이면 dp에서 뺄셈을 진행하면서 나아가야한다.

i = 2 인, 2개를 고려하는 상태에서 2개의 수를 선택한다고 했을때, 무조건 짝수번째 수는 빼고 홀수번째 수는 더해야한다. 그런 연산 속에서도 최대값을 구해야하는 것이므로, max로 감싼다. 따라서 점화식은 다음과 같게 된다.

문제 2
- 숫자가 쓰여있는 빨강, 파랑 공이 각각 N 개 있고 매 선택마다 무조건 하나의 색의 공만을 골라야 한다고 한다(첫 선택에서 빨간 공을 고르면 다음 선택으로 넘어가야한다. 빨강 공과 파랑공을 동시에 선택할 수 없다) 각 색깔의 공을 각각 N개씩 골랐을 때, 공에 쓰여있는 숫자의 합이 최대가 되도록 하기
ex. N = 2, RED = { 5, 5, 6, 3}
BLUE = {4, 2, 4, 3}
문제링크: https://www.youtube.com/watch?v=vbKgB56mIA0&t=163s
비교해야할 대상
- 내가 지금까지 몇 개를 골랐는가? = i index, → i == 2N에서의 최댓값을 리턴할 것.
- Dynamic programming = bottom-up. 문제를 잘게 쪼갠다.
즉, 두 번째로 비교해야할 대상은, 내가 지금 몇 개의 빨강 공을 골랐는가? = j index
초기값
나의 접근 - 잘못된 접근)


이 문제 또한 이중배열로 풀 수 있다.
고려해야하는 것은 지금까지 몇 개를 골랐는가?(== i) 와 지금까지 빨간색은 몇 개 골랐는가?(== j) 이다.
무조건 하나는 선택해야하는 문제이므로 빨강을 고른 것이 아니라면 파란색 공을 고르게 되는 것이다. 정답은 따라서 DP[2N][N]이 된다.
총 2개를 고르는 단계에서(i == 2, RED[2]를 넣을지 BLUE[2]를 넣을지 고민하는 단계)
1개를 이미 골라둔 상태에서 빨간 색 공을 고를지 vs 파란색 공을 고를지 max 비교한다.
빨간색 공을 고르는 경우라면, DP의 j가 빨간 색 공의 개수를 의미하므로 DP[i-1][j-1]로부터 값을 가져와야한다.

String Matching - 이건 어떻게 DP로 푸는건지조차 감이 안 잡히는 문제. 상당히 어렵다!
사실 DP는 경로는 상관 없다. 최대던 최소던 값만 나오면 되는 것이다(여기서 그 경로를 출력하라고 하면 그건 또 다른 문제이긴 하다)
주어진 string들의 부분 수열이 모두 들어가야 한다. A, B의 문자열의 길이를 1부터 늘려가면서, 나올 수 있는 최단 공통수열의 길이를 구하기 위해서는 무조건 하나 이상의 알파벳이 더해져야한다. A[i] == B[j] 일 경우에는 이전 최솟 값(dp[i-1][j-1]에서 +1을 하면 되지만(같은 알파벳이므로 하나만 더하면 된다), 같지 않을 경우에는 (이전까지의 최단 공통수열이 무엇인지는 모르겠지만) 어떤 최단에다가 새로운 알파벳(A[i]혹은 B[j]) 를 더해야 최단이 될 지를 고민해야 한다.
여기서 하나만 더해도 되는 이유는, 이미 이전 인덱스에서 계산한 것을 바탕으로 A 혹은 B 중 하나만 늘려서 최단을 계산하려고 하는 것이기 때문이다.
예시문제 1. 주어진 두 문자열을 모두 부분수열로 갖는 수열 중 최단 길이의 수열의 길이를 구하시오.
(모두 부분수열로 갖는다 = 연속해있지 않아도 어느 위치에는 주어진 문자열이 순서대로 포함되어 있다)







오르막 수, 점프
어려웠던 문제 1. 정수 사각형 최댓값의 최소
어려웠던 문제 2. 동전 2