필요한 개념
수학
선형독립, Span, 표준행렬, 부분공간, 계수, 벡터
AI
Back propagation, Sigmoid, CNN 필터 연산, RNN 네트워크 구성, Pooling ?
정규화 방식, Gradient descent 종류 및 차이, overfitting & underfitting
보충 및 정리
수학
베이즈 통계학
- 조건부 확률


- 1종오류 = False Positive
2종 오류 = False Negative 질병이 아니다라고 판단했지만 실제론 질병인 경우.
암 환자 진단 시 False Negative를 더 신경써야 한다(줄여야 한다) - 정밀도(Precision): TP/(TP+FP) 여기서 FP는 오탐지율(False positive)를 의미하며, 이를 줄일 경우 정밀도 상승.
민감도(Recall): TP/(TP+FN) 모델이 positive라고 판단한 것 중 Posiitve인 것. 암 환자 진단 시 이 민감도를 높여야 한다(=FN을 줄여야 한다) - 베이즈 정리를 이용해 사후확률을 가지고 갱신된 사후확률을 계산할 수 있다(Posterior). update를 통해 예측력 상승.
업데이트 된 정보를 가지고 확률 계산을 하므로 예측 정확도가 높아진다.
즉, 1st에서는 사전확률 P(B)를 가지고 계산했다면, 2nd에서는 P(B|A)라는 사후확률이 계산되어있으므로 P(B):=P(B|A)로 업데이트 하고 계산. - 조건부확률을 가지고는 인과관계를 추론해서는 안 된다(데이터가 많아져도 불가능)
대신 데이터의 관계가 달라지는 인풋이 들어온다면 인과관계 기반인 모델이 테스트 결과가 robust하게 된다.
(대신 높은 정확도를 보장하긴 힘들다) - 인과관계에 대한 연관성을 알기 위해서는 중첩요인을 제거해야한다.

선형대수 - 선형시스템과 역행렬
- linear equation: ax = b, a, x는 컬럼벡터. b는 constant
linear system은 linear equation으로 구성됨. 선형연립방정식. Matrix equation. - Identity Matrix = 항등 행렬. 정사각 모양. 대각선 성분은 모두 1이다. 2차원 역행렬 1/(ad-bc)[d -b/-c a]
직사각행렬은 역행렬의 교환법칙 (A-1A = AA-1) 이 성립하지 않는다.\ - 역행렬이 존재 = 근이 1개만 존재. 근이 하나만 존재하지 않는다면 x*와 같은 답으로 나오지만, 결국 x*=x가 된다(A-1A에 의해 Identity가 된다)
역행렬이 존재하지 않는다면(ad-bc = 0이라면. 이는 즉 determinant. det(A) = 0 이라는 것. 등식이 성립하면 역행렬 존재X)
3*3 determinant는 아래와 같이 구한다.



- Determinant: 선형변환에서의 데이터, 벡터의 길이를 얼마나 scalar형태를 취했느냐를 detminant로 계산할 수 있게 된다.
3*3이상은 gaussian elimination을 이용해서 구한다.
역행렬이 존재하지 않는다면, 선형연립 시스템에서 해가 무수히 많거나(두 방정식이 동일), 해가 아예 없게 된다(두 방정식이 평행) - 데이터의 개수보다 feature 개수가 많을 때: 방정식의 개수가 미지수의 개수보다 적은 것. under determined system. 무수히 많은 해 -> 머신러닝에서는 regularizaion을 활용한다. 음... 가장 coefficient가 작은 걸 선택하게 한다거나...
- 데이터의 개수가 feature 개수보다 많을 때: 방정식의 개수가 더 많은 것. over determined system. 해가 존재하지 않음.
선형 대수 - 선형 결합
- linear combination: 가중치는 일반적으로 실수를 사용.
linear system에서 matrix연산은 column으로 나누어 선형 결합으로 만들 수 있다.

- 그러면 이는 벡터방정식으로 표현이 된다. 이 때 Ax=b 에 해가 존재할지를 파악할 수 있다.
- "Span": span is defined as the set of all linear combinations of v1, v2, ... vp. 가능한 모든 선형 결합벡터의 집합.
v1, v2 얘는 공간상에서 하나의 평면이 span이 된다.
선형독립인 v1, v2, v3 얘는 평행사변형의 꼭지점이 연장되서 ... 모든 점들이 span안에 들어간다. 3차원이 span.
벡터방정식의 해가 존재할 지를 span을 통해서 확인할 수 있다. b라는 벡터가 A column vector로 만들어지는 span안에 있다면 해가 존재한다는 의미이다.
The solution exists only when b is in Span{a1, a2, a3} - Matirx multiplication = Sum of outer product 라고 볼 수 있다(각 Matrix를 column으로 분할하는 것.
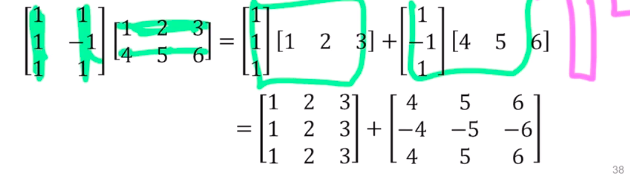
- 이 sum of outer vector로 한다면 차원축소, 파라미터 수 줄이기 등의 이득을 볼 수 있는듯.
untangle data into independent components!
https://jonathan-hui.medium.com/machine-learning-singular-value-decomposition-svd-principal-component-analysis-pca-1d45e885e491
선형대수 - 선형독립과 종속
- 선형독립인 경우 선형방정식은 유일한 해를 가진다.
Span 안에 상수벡터가 존재하면 해가 존재한다고 했는데, 이는 유일한 해라면, linear independent.
v라는 벡터가 span 안에 존재한다면, 선형종속이 된다(여러 평면을 만들 수 있다... span을 늘려주는 게 아니면, 기존 span은 선형 종속이 된다.)
해가 여러 개 존재한다 = 평행사변형을 여러 개 만들 수 있다는 의미.

- 방정식보다 feature가 더 많으면 무수히 많은 해!
Ax = 0 인 식을 homogeneous 라고 한다.
A linearly dependent vector does not increase Span! 선형 종속인 벡터가 포함되면 span은 증가하지 않는다.
(span의 차원이 증가하지 않는다고 이해하면 될 듯. 동일한 평면으로 머무른다.)


- 선형 종속인 시스템이라면 multiple possible 의 해가 존재한다. b가 0일 때 해가 있다면, b가 0이 아니어도 여러 해가 존재.
선형대수 - 부분공간, 기저, 랭크
- 부분집합은 subset이라는 개념 + 선형결합에 닫혀있는 것. 연산에 대한 결과가 모두 해당 집합안에 있음.
Span 이라는 것과 유사함. Span 이라는 것은 항상 subspace이다. 부분공간은 항상 span으로 표현된다. - 기저(Basis): 기저는 부분공간 H를 fully 표현하고, linearly independent 하다. 기저벡터는 해당 공간을 대표하는 단위벡터.
기저벡터는 유일하지 않다. 다른 벡터가 충분히 H를 표현할 수 있음.
Dimension of Subspace는 유일하다. dimension = basis 의 개수 - column space: 컬럼 벡터로 이루어진 span -> column span.
- 행렬의 Rank(계수): Rank A = dim(Col(A)).
선형대수 - 선형변환
- bias term이 있는 방정식은 선형 시스템이 아니지만, 상수를 벡터 안에 넣게되면 선형 시스템으로 만들 수 있다.
- Standard matrix = 벡터의 차원을 줄이는 어떠한 행렬 T가 있을 때, 기저벡터로 표현된 T를 Standard Matrix라고 한다. 아래 사진 참조.

선형대수 - Neural network 선형변환(선형대수 - 6th lecture)
교수님 수업시간에 대부분 배운 것. 기저 벡터의 선형변환을 차원 상에서 어떻게 해석할 수 있는가? 에 대한 내용.좌표에 대한 distortion. 직사각형 -> 기울어진 평행사변형 등... 평면의 distortion이 일어난다~
y = 3x + b 는 선형변환이 아님~!(이전 강의에서 말씀하셨단다. 이것 자체로는 Affine transformation 이라고 한다. 1이라는 bias term을 넣으면 선형변환이 된다는디? 아 알거같은데 들어봐야하네. linear combination으로 변환?? 아~~~ ok.
bias term 을 W로 합쳐버릴 수 있도록, 계산 상의 팁이 있음.11:45. input feature dimension의 마지막에 끼워넣고 linear라고 본다(==linear combination))
Fully-connecte layer = Affine layer.
Numpy
1. 코드로 방정식 표현 -> 리스트로 간단히 가능하지만, 다양한 매트릭스 계산에 어려움. python 처리속도가 오래걸림
리스트는 메모리의 주소를 연결하는 구조라서 메모리 효율이 떨어짐.
2. 개념 Numpy: Numerical Python. 파이썬의 고성능 과학 계산용 패키기. Matrix와 Vector의 Array연산에 쓰임
리스트에 비해 메모리 효율적. 반복문 없이 데이터 배열에 대한 처리 지원. c, c++, 포트란 등과 통합 가능.
3. import numpy as np -> as=alias
numpy -> ndarray 객체 생성, 한 가지 데이터 타입만 지원. Dynamic typing not supported
4. numpyt array는 데이터가 메모리에 차례로 들어간다(할당). 메모리도 일정함.
python list는 -5~256까지의 값이 메모리의 static 한 공간에 저장되고, 리스트에는 값의 주소값이 저장된다. 그래서 리스트는 변형이 쉽지만, 처리 속도가 길어진다. 같은 값에 대한 주소값을 기준으로 하기 때문에, 다른 리스트의 같은 값을 비교하면 True 가 리턴된다(nparray는 그렇지 않음)

5. shape = dimension(tuple 형태로 리턴), dtype = data type
0 dim = scalar, 1 dim = vector, 2 dim = matrix, 3 dim~ = n-tensor
(4, 3, 4) = 4 채널 3 row 4 col tensor. n~ 차원이면 () 의 앞 부분에 추가됨.
6. float32 = 32bit, int8 = 8bit = 1byte. np.array의 메모리 사이즈 계산이 가능(np.array().nbytes)
7. Handling shape
- np.array.reshape는 reshape결과가 리턴될 뿐, 변형이 일어나지 않는다.
- indexing: [0, 0] 와같은 comma 표기법 가능
- slicing: [:, :2] = col에 대해 0~1col 만 추출. a[1:3] = 2dim, a[1] = 1dim, start point: endpoint : 간격(step) ex. arr[::2, ::3]
8. Creation function
- np.arange(start, end, step) floating step 도 가능함.
- np.zeros(shape, dtype, order)
- np.empty(shape, dtype, order) # memory initialize 가 일어나지 않음. 공간만 만드는거라 이전 값들이 남아있을 수 있음.
- np.something_like(기존 array), np.identity(number of rows, dtype), np.eye(row size, col size, k=1시작 위치) # 대각행렬
np.diag(기존 행렬, k=추출 위치) # k 위치부터 대각성분 추출
- np.random.uniform(시작, 끝, 개수) # 균등 분포, np.random.normat # 정규분포
9. Axis: 차원이 추가될 때마다 axis 는 뒤로 밀려남. 2dim (3, 4) axis 0: 3, axis1 = 4, 3dim (3,3,4) axis0 = 3, axis1 = 3 ... 새롭게 추가되는 랭크(차원)이 axis 0이 되고 뒤로 조금씩 밀려난다.
10. vstack, hstack, concatenate: axis기준. [np.newaxis, :]로 축 추가가 가능
11. operation: element-wise 연산이 가능. 동일한 크기의 array에 * 하면 element wise가 됨.
dot product = matrix.dot(another matrix)
broadcasting: 크기가 다른 matrix, vector에 대해서도 크기가 자동으로 맞춰져서 연산이 됨(* 곱하기도 포함)
%timeitdms 쥬피터에서의 시간 소요 확인
12. Comparison
- '>' or '<': np.any(a>5) 를 통해 a의 모든 원소에 대해 >5 가 True인지 판단. np.all(a<5)
- np는 크기가 동일하면 elementwise 비교가 가능 a > b 라고 하면 a크기만큼의 comparison operation.
- np.logical_and와 같이, boolean type np에 대한 비트연산 가능
- np.where(condition, return TRUE value, return FALSE value)
np.where를 통해 condition에 True인지 아닌지(element wise) 파악도 가능하다(리턴 = index)
- np.argmax, np.argmin 도 index를 반환. axis=1 이라고 하면 column이지만 -> 방향이라 row별 max min index 리턴
- np.argsort또한 인덱스를 원소로 가짐.
경사하강법(순한맛) : 미분 값을 빼는 것.
- import sympy as sym / sym.diff(sym.poly(x**2 + 2*x +3), x) 와 같이 라이브러리로 가능
- 변수가 벡터이면 편미분 진행. from sympy.abc import x, y ...

- 그래디언트 벡터: 가장 빨리 증가하는 방향으로 화살표가 그려짐 -> - nabla f = 마이너스 이므로, 가장 빨리 감소하는 방향으로 그려짐(극소점 방향)
- while(norm(grad) > epsilon): # 벡터의 그래디언트 계산 종료조건은 norm으로 한다.
# gradient 계산
AI
1. Gradient Descent Methods
- SGD(stochastic gradient descent): 엄밀히 말하면 하나에 대해서 gradient를 구해서 update.
- Mini-batch gradient descent: 10만 개 중 mini batch(ex. 100개) 단위 계산 update
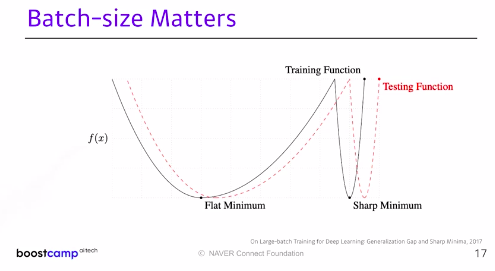
large batch methods -> sharp minimizers로 수렴하는 경향이 있다.
small batch methods -> flat minimizer로 수렴한다. small batch가 더 낫다(최솟값의 함수 형태가 좀 더 flat.)
2. automatic differentiation

- Stochastic Gradient Descent: 랜덤으로 배치사이즈를 결정하고 lr을 계산해 서치함. learning rate 를 적절히 선정하기 어렵다는 단점 존재.
- Momentum: 관성, 운동량을 기준으로 gradient를 계산하고 update. t-1 시간의 gradient를 계속 가지고 있음(accumulate. 관성)


- Nesterov Accelerate: gradient 계산 시 lookahead. 모멘텀과 다르게, 한번 미리 계산한 값을 가지고 연산, 빠르게 converge.
local minimum으로 모멘텀이 converge 잘 못하기 때문에. local minimum을 빠르게 찾음(converge ratio가 빠름)
- Adagrad(adaptive.): 뉴럴 네트워크의 파라미터가 얼마나 변했는지를 반영. 지금까지 많이 변화한 파라미터는 덜 변화시키고, 지금까지 덜 변화한 파라미터는 적게 변화시키겠다(gradient 제곱의 합을 루트로하고 분모로 함) 안 변한 파라미터를 많이 변화시킴. 대신 뒤로 갈 수록 값이 0에 가까워져 학습이 이뤄지지 않는다(학습률은 아마도 이전 기울기의 누적 제곱 합에 반비례)

- Adadelta: (반영하고자 하는 그래디언트를 윈도우 사이즈만큼의 gradient 제곱만 계산하겠다~. 파라미터의 개수에 따라 연산이 많아질 수 있음.) 그래서 Adadelta는 exponential moving average of Gradient를 통해서 large Gt를 계산함. 얘는 그래서 no learning rate. 많이 쓰이지 않음.

- RMSprop(Root Mean Square Prop): 제프리 힌턴의 수업에서 나옴. Exponential Moving Average of Gradient squares(제곱)
Adagrad에서의 sum of gradient square에 EMA를 넣은것. Adadelta에 없는 stepsize 존재(아마도 EMA로 이전 기울기를 더 크게 반영)

- Adam: Adaptive Momentum Estimation. 그래디언트의 크기에 따른 EMA와 이전 그래디언트들의 모멘텀을 합친 것.


2. Regularization: generalize performance 향상
- 규제. 모델이 test에도 잘 되게끔.
- Early Stopping: validation error가 커지는 시점에서 stop.
- Parameter Norm Penalty: 파라미터규제. loss function에 파라미터 값을 더해서 파라미터
함수를 부드럽게 만든다(smoothness to the function space). = weith decay
- Data Augmentation: 데이터가 많아야 함.
- Noise Robustness: 뉴럴네트워크 웨이트에도 noise를 넣는 것. 실험적으로 나타난 것. input data에도 노이즈를 섞는걸 포함.
- Label Smoothing: decision boundary를 좀 더 부드럽게 한다고 생각하심. CutMix: cat 사진과 dog 사진을 잘라 합침. 라벨을 cat 0.5 dot 0.5로 주는 것. mixup은 두 이미지를 흐리게 해서 합성하는 것. 성능이 많이 올라간단다.
- Dropout: randomly set neurons to zero. train에만 적용. test에는 모든 노드가 켜진다. 여러 모델을 합친 결과와 비슷한 결과를 낸다.
- Batch Normalization: 네트워크 레이어 사이의 값을 정규화 하는 것. mean zero, unit variance를 가지게. internal covariate shift를 줄인다고한다지만 논란이 있음. 계층간 학습이 잘 됨.
batch norm, layer norm, instance norm, group norm이라는 normalization technique가 여러 종류 존재.
CNN(Convolution Neural Network)
- RGB Image Convolution: filter의 채널은 RGB 3채널을 갖는다. 커널(=filter)의 개수가 output feature의 채널개수가 된다.
- CNN & pooling layer: feature extraction, Fully connected layer: decision making(ex. classification)
- 파라미터 숫자에 dependent -> 요즘은 Fully connected layer가 줄어드는 추세이다. 파라미터 숫자가 많아질 수록 generalization perfomance가 떨어진다고 알려져있기 때문. Network는 deep 하게 만들지만, 파라미터 숫자는 줄이도록 한다.
- Stride: 필터를 이동하는 칸 수. Padding: boundary 정보를 저장하기 위해 input에 추가하는 칸 수(zero padding)
- 파라미터 수 연산: (H, W, C) = (40, 50, 128) 에 3*3 커널으로 (40, 50, 64)을 만드려면 필요한 파라미터 수는?(padding=1. stride = 1)
커널의 채널 = 인풋 이미지의 채널임에 주의. -> 커널은 (3, 3, 128, 64) = 73,738. 스트라이드와 패딩은 상관없다.
몇 만 단위인지 감을 잡고 있는 게 필요하다.


- Dense layer: 하나의 커널이 모든 위치에 동일하게 적용되기 때문에 파라미터 수가 많아진다. 커널은 shared operation으로 동작하게 된다.
Dense layer: input parameter * output parameter 개수 이다. 위 사진에서 dense layer 직전의 레이어는 13*13*128 이 2개 있었다. output으로 2048 개의 output feature를 "각각" 추출하고 싶은 것이므로, 13*13*128*2*2048*2 = 177M이 된다.
- 1*1 layer: channel이 1*1*128*32 처럼... dimension reduction에 사용됨. To reduce the number of parameters while increasign the depth. ex) bottleneck architecture.
*참고 bottleneck architecture: input의 채널을 (1*1 연산으로)줄인 뒤 convolution 연산을 수행해서 feature map의 수를 증가시킨 뒤, 다시 1*1로 채널을 증가시키는 것.

- bottleneck 없이 하면 3*3*256*256 이지만, 줄이고 하면 3*3*64*64 로 네트워크 계층은 깊게 하되 파라미터 수를 획기적으로 줄일 수 있다(대신 정보 손실이 일어남)
RNN - 정의와 종류
- Sequential model: t-1, t-2, ... time 이후에 t time의 데이터의 조건부확률 = Naive sequence model. 정보량증가
- 어느정도의 길이의 input일지를 알 수 없어 CNN X
딥러닝 학습방법 - 소프트맥스
- 오버플로우 방지를 위해 np.max를 이용해서 계산했음
추론의 경우에는 소프트맥스를 굳이 쓰지 않고 그냥 원-핫 벡터만을 사용한다.

- MLP - 층이 깊을 수록 목적함수를 근사하는 데 필요한 뉴런의 숫자가 빨리 줄어든다고 한다(효율적인 학습)
그냥, 층이 얇으면 넓은 학습망을 만들어야하니까 그런 듯. - Backpropagation


참고한 사이트